1. 순열(Permutation)
서로 다른 n개중에 r개를 선택하여 정렬하는 경우의 수
- 정렬은 r개를 택하여 일렬로 배열하는 경우를 말한다.
- [1, 2, 3]과 [3, 2, 1]은 다른 것.

static boolean[] visited;
static int[] result;
public static void main(String[] args) {
int[] arr = {1, 2, 3};
int r = 2;
visited = new boolean[arr.length];
result = new int[r];
permutation(arr, 0, r);
}
public static void permutation(int[] origin, int depth, int r) {
if (depth == r) {
for (int i = 0; i < result.length; i++) {
System.out.print(result[i] + " ");
}
System.out.println();
return;
}
for (int i = 0; i < origin.length; i++) {
if (!visited[i]) {
visited[i] = true;
result[depth] = i;
permutation(origin, depth + 1, r);
visited[i] = false;
}
}
}
재귀의 2step을 보면, 이미 선택된 숫자들은 쳐다보지 않는다.
2. 중복 순열 (permutation with repetition)
서로 다른 n개중에 중복이 가능하게 r개를 선택하여 정렬하는 경우의 수
- 순서대로 일렬로 배열하는 것은 동일하지만, 동일한 원소도 중복해서 선택할 수 있다는 차이가 있다.
- [1, 1, 1], [2, 2, 2]가 가능하다.
static int[] result;
public static void main(String[] args) {
int[] arr = {1, 2, 3};
int r = 3;
result = new int[r];
permutation(arr, 0, r);
}
public static void permutation(int[] origin, int depth, int r) {
if (depth == r) {
for (int i = 0; i < result.length; i++) {
System.out.print(result[i] + " ");
}
System.out.println();
return;
}
for (int i = 0; i < origin.length; i++) {
result[depth] = i;
permutation(origin, depth + 1, r);
}
}
3. 조합(Combination)
서로 다른 n개에서 r개를 뽑는 방법의 수(순서 상관 없음)
- 순서가 상관없다는 말은 [1, 2, 3]과 [3, 2, 1]은 같다는 말

static boolean[] visited;
static int[] result;
public static void main(String[] args) {
int[] arr = {1, 2, 3};
int r = 2;
visited = new boolean[arr.length];
result = new int[r];
permutation(arr, 0, 0, r);
}
public static void permutation(int[] origin, int depth, int start, int r) {
if (depth == r) {
for (int i = 0; i < result.length; i++) {
System.out.print(result[i] + " ");
}
System.out.println();
return;
}
for (int i = start; i < origin.length; i++) {
if (!visited[i]) {
visited[i] = true;
result[depth] = origin[i];
permutation(origin, depth + 1, i + 1, r);
visited[i] = false;
}
}
}
언뜻보면 순열과 비슷하지만, 이미 지나온 값은 탐색하지 않는다는 차이가 있음.
다음 재귀의 start는 현재 값(인덱스)의 + 1이다.
4. 중복 조합(Combination with repetition)
서로 다른 n개에서 중복이 가능하게 r개를 뽑는 방법의 수
- 순서가 상관없는 조합과 동일하지만, 이미 뽑은 것을 다시 뽑을 수 있다는 점에서 차이가 있음.
static int[] result;
public static void main(String[] args) {
int[] arr = {1, 2, 3};
int r = 2;
result = new int[r];
permutation(arr, 0, 0, r);
}
public static void permutation(int[] origin, int depth, int start, int r) {
if (depth == r) {
for (int i = 0; i < result.length; i++) {
System.out.print(result[i] + " ");
}
System.out.println();
return;
}
for (int i = start; i < origin.length; i++) {
result[depth] = origin[i];
permutation(origin, depth + 1, i, r);
}
}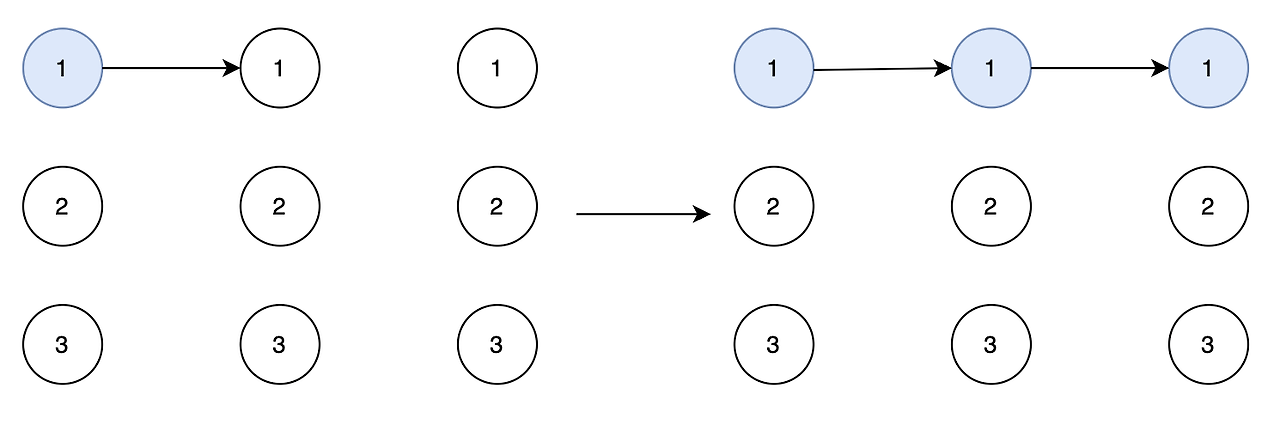
중복 순열과 동일해 보이지만 [1, 2, 1]이 가능한 중복순열과 달리 이미 지난 수는 선택하지 않는게 중복 조합 특징.
자기 자신을 다음 재귀에 한번 더 선택할 수 있다고 생각하면 쉬움.
반응형
'알고리즘 | 자료구조' 카테고리의 다른 글
| [알고리즘] Union-Find 알고리즘 (Disjoint Set) (0) | 2020.09.06 |
|---|---|
| [알고리즘/정렬 알고리즘] 병합 정렬(Merge sort) Java, Python (0) | 2020.06.28 |
| [알고리즘/정렬 알고리즘] 퀵 정렬(Quick sort) Java, Python (0) | 2020.06.28 |
| [알고리즘/정렬 알고리즘] 셸 정렬 (Shell sort) Java, Python (0) | 2020.06.28 |
| [알고리즘/정렬 알고리즘] 삽입 정렬 (Insertion sort) Java, Python (2) | 2020.06.27 |