Disjoint Set?
디스조인트 셋은 서로 중복되지 않는 부분 집합들로 나눠진 원소들에 대한 정보를 저장하고 조작하는 자료 구조이다.
Distjoint Set - 서로소 집합
Union-Find?
Disjoint Set을 표현할 수 있는 알고리즘
집합을 구현할 때 벡터, 배열, 리스트 등을 사용할 수 있으며, 주로 트리구조와, Hash구조(대량)을 사용하여 구현한다.
Union-Find 연산
1. Make-Set(x)
- 집합들을 초기화하는 원소로, 집합에는 x만 있을 수 있게, 즉 유일한 원소로 하는 집합(들)을 만든다.
2. union(x, y)
- 집합들을 합치는 용도로, x와 y가 포함된 두 집합을 합치는 연산
3. find(x)
- 루트, 최상의 부모노드(=루트, 같은 말) 찾기, x가 어떤 집합에 속해있는지 찾기 위해 그 집합을 대표하는 루트 노드, 최상위 부모를 반환한다.
[예시]
1. Make-Set

| Element(Parent) | 0 | 1 | 2 | 3 | 4 |
| index | 0 | 1 | 2 | 3 | 4 |
2-1. Union(0, 2)

| Element(Parent) | 0 | 1 | 0 | 3 | 4 |
| index | 0 | 1 | 2 | 3 | 4 |
2-2. Union(2, 4)

| Element(Parent) | 0 | 1 | 0 | 3 | 2 |
| index | 0 | 1 | 2 | 3 | 4 |
3. Find(4)

Find(x)를 했을 때, x가 포함된 최상위 부모 노드를 찾는다고 했다.
1 : 4의 부모노드는 2
2 : : 2의 부모 노드는 0
즉, 0을 반환한다.
[코드]
Union, 연산 최적화 Union, 두 원소가 속한 트리의 전체 노드 수 구하는 Union
find, 경로압축 find를 포함합니다.
1. 기본 Union, find
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
public class Union {
static int[] elements;
public static int find(int x) {
if(elements[x] == x) { //집합에 자기 자신만 있거나, x가 최상위 노드거나
return x;
}else {
return find(elements[x]); //최상위 노드를 찾을 때 까지 재귀적으로 탐색
}
}
public static void union(int x, int y) {
x = find(x);
y = find(y);
elements[y] = x; //y의 부모는 x이다.
}
public static void main(String[] args) {
elements = new int[10];
for(int i = 0; i < elements.length; i++) { //Make-Set
elements[i] = i;
}
//0, 1, 2, 3, 4, 5, 6, 7, 8, 9
union(0, 9); //9 -> 0
union(9, 4); //4 -> 9
System.out.println("4의 최상의 부모노드는 "+find(4)+"입니다.");
System.out.println("-------모든 요소 출력--------");
for(int i = 0 ; i < elements.length; i++) {
System.out.println(i +" -> "+elements[i]);
}
}
}
|
cs |
/*결과*/
4의 최상의 부모노드는 0입니다.
-------모든 요소 출력--------
0 -> 0
1 -> 1
2 -> 2
3 -> 3
4 -> 0
5 -> 5
6 -> 6
7 -> 7
8 -> 8
9 -> 0
2. 경로 압축 find
|
1
2
3
4
5
6
7
|
public int find(int x) {
if(elements[x] == x) {
return x;
}else {
return elements[x] = find(elements[x]); //경로를 지나는 모든 부모 노드를 최상위 부모노드로 바꿈
}
}
|
cs |
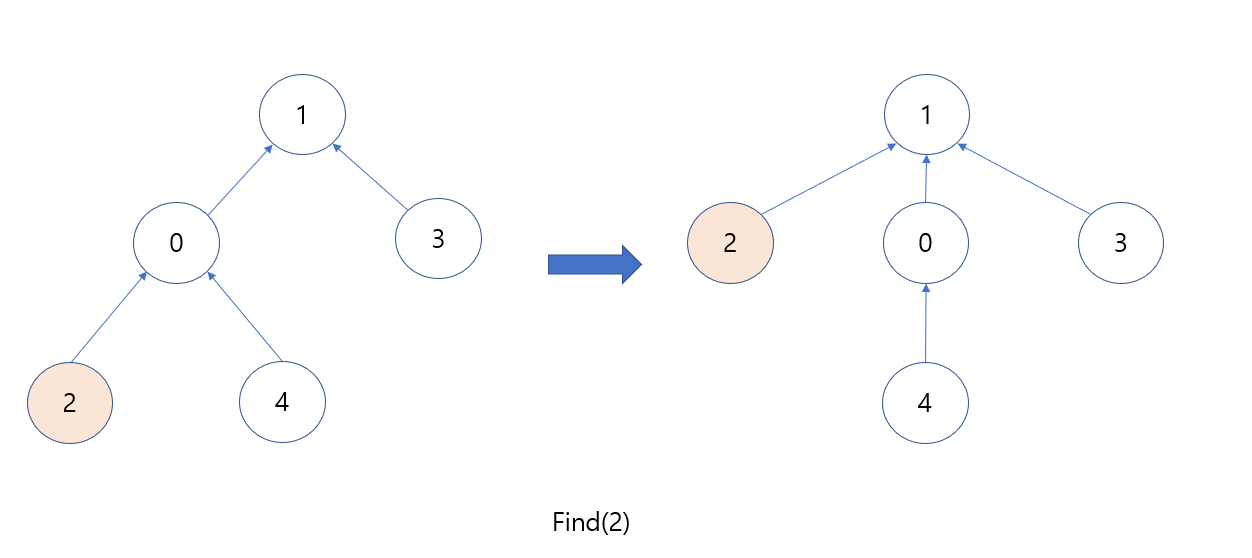
3. 연산 최적화 Union - 트리 높이가 작은 트리는 높은 트리의 밑으로 연산된다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
//main 부분 rank는 클래스 변수로 선언 후 main에서 크기 할당.
rank = new int[10];
for(int i = 0; i < 10; i++) {
rank[i] = 0; //높이를 0으로 초기화
}
public void union2(int x, int y) {
x = find(x);
y = find(y);
if(x == y) //부모가 같으면 같은 집합.
return;
if(rank[x] < rank[y]) { //y가 더 큰 높이를 가진 트리라면. union-by-rank 최적화
elements[x] = y; //y 밑에 x를 붙힘
}else {
elements[y] = x;
if(rank[x] == rank[y]) { //높이가 같아 한쪽이 밑으로 들어오면 +1 만큼 깊어짐.
rank[x] += 1;
}
}
}
|
cs |
4. 두 집합을 Union 한 뒤, 전체 노드 수 구하기
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
//main 부분 nodeCnt는 클래스 변수로 선언 후 main에서 크기 할당.
nodeCnt = new int[10];
for(int i = 0; i < 10; i++) {
nodeCnt[i] = 1;
}
public int union3(int x, int y) {
x = find(x);
y = find(y);
//x가 y보다 더 크다고 가정
if(x != y) { //다른 집합이면
elements[y] = x; //y -> x
nodeCnt[x] += nodeCnt[y];
nodeCnt[y] = 1; //x에 붙은 y값은 1로 초기화
}
return nodeCnt[x];
}
|
cs |
1~4번뿐 아니라 원하는 방식대로 다양하게 로직을 구현할 수 있습니다.
**게시글 중 로직 오류 또는 개선하면 좋을 점에 대해 피드백해주시면 정말 감사하겠습니다.
참고 자료 :
ratsgo.github.io/data%20structure&algorithm/2017/11/12/disjointset/
gmlwjd9405.github.io/2018/08/31/algorithm-union-find.html
'알고리즘 | 자료구조' 카테고리의 다른 글
| 순열, 중복순열, 조합, 중복조합 (Java) (1) | 2024.02.13 |
|---|---|
| [알고리즘/정렬 알고리즘] 병합 정렬(Merge sort) Java, Python (0) | 2020.06.28 |
| [알고리즘/정렬 알고리즘] 퀵 정렬(Quick sort) Java, Python (0) | 2020.06.28 |
| [알고리즘/정렬 알고리즘] 셸 정렬 (Shell sort) Java, Python (0) | 2020.06.28 |
| [알고리즘/정렬 알고리즘] 삽입 정렬 (Insertion sort) Java, Python (2) | 2020.06.27 |